rollo ha scritto:dindy una domanda: fa finta che io sia un bambino di 6 anni, cos'è la fase ? grazie.
Provo ad estendere la risposta di Mario Bon, però bisogna spostarsi dalle elementari almeno fino alle superiori, perché un po' di trigonometria è necessaria.
In particolare è necessario partire dalla funzione seno, che è una funzione strettamente legata alla circonferenza, come si può vedere in questa utile animazione di Wikipedia:
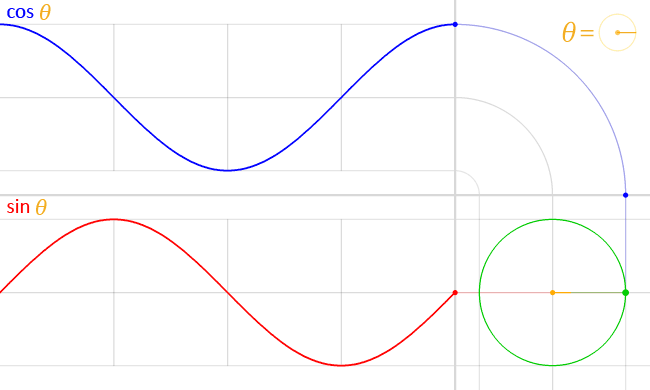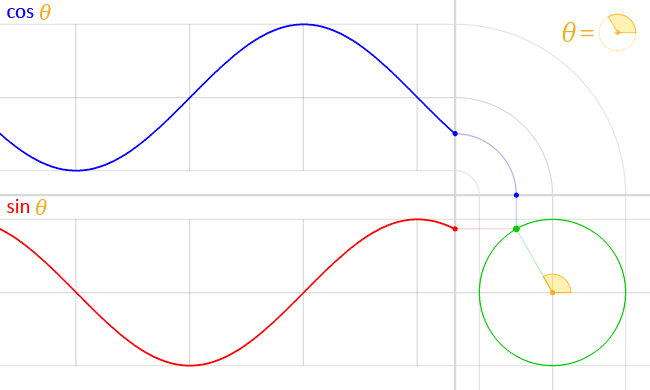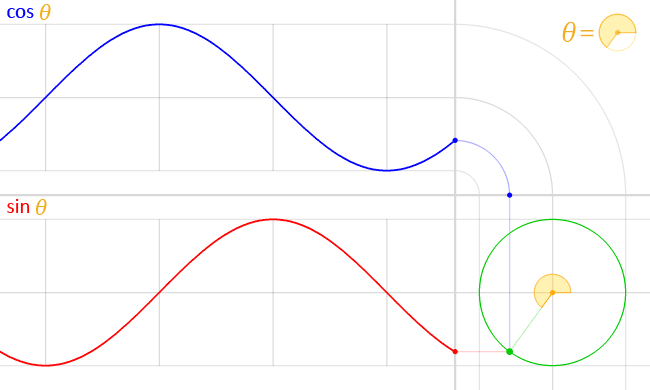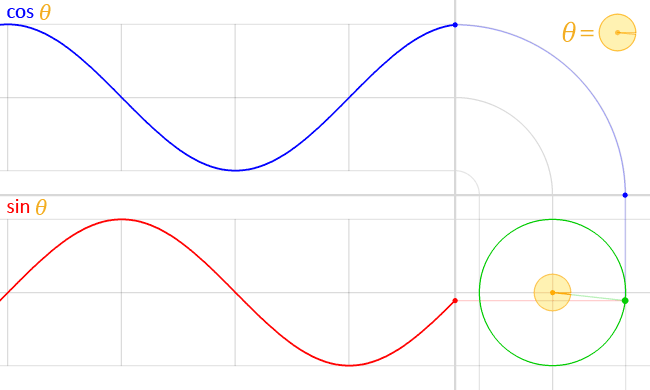
A noi interessa la funzione rossa, che è sostanzialmente la distanza della punta della lancetta di un orologio (che gira al contrario) dall'asse delle x in funzione della posizione della lancetta, definita dall'angolo rispetto allo stesso asse delle x. Servirebbe anche l'altra funzione, ma poi diventa troppo complesso. Se si estende la funzione y = sin(phi) e si aggiungono un po' di costanti si può ottenere la seguente funzione:
y = a * sin(w * t + p)
a è l'ampiezza dell'oscillazione, ossia il raggio del cerchio.
w è la velocità angolare ed è legata alla frequenza tramite la semplice relazione w = 2 * pi * f, dove f è la frequenza. Ti dice quanto veloce è la rotazione e di conseguenza quanto diventa fitta la sinusoide nel tempo, indicato con t.
p è la fase iniziale e sostanzialmente ti dice dove si trova la lancetta per t = 0, ossia all'istante inziale. E' il punto da cui si parte.
Con queste costanti in buona sostanza si possono rappresentare tutte le sinusoidi possibili, più o meno fitte, più o meno ampie e che partono da un qualunque punto iniziale.
Fin qui sembra un giochino per matematici impenitenti, ma il punto chiave è che questa funzione può essere presa a riferimento quale esempio paradigmatico di funzione periodica, ossia di funzione che si ripete uguale ogni tot tempo. Di queste funzioni se ne incontrano spessissimo nella realtà, per cui sono piuttosto importanti.
Qui entra in gioco il buon Jean Baptiste Fourier, matematico francese che in questi giorni non riesce a trovare pace nel suo giaciglio al cimitero del Père-Lachaise. Il buon Fourier infatti ha dimostrato che qualunque funzione periodica che soddisfa un minimo di requisiti può essere scomposta in una "somma" di sinusoidi con appropriata ampiezza, frequenza e fase iniziale (La formulazione esatta è più complessa, richiede appunto l'uso dei numeri complessi, in più esistono diverse trasformate di Fourier, discreta, continua, periodica, etc, ma se ti interessa approfondire non bastano più le superiori e ti tocca studiare. Qui mi limito ad una generica descrizione intuitiva, che a rigore è sbagliata.). Il legame tra la funzione inziale e la scomposizione è biunivoco, ossia dato un segnale esiste una e una sola scomposizione possibile e viceversa. Sono due modi diversi di vedere la stessa cosa e se modifichi una modifichi anche l'altra.
Qui si comincia ad uscire dal giochino per matematici e si comincia ad entrare nel pratico. Gestire qualcosa che oscilla lentamente è ovviamente differente dal gestire qualcosa che oscilla rapidamente. Se hai un fenomeno complesso che si ripete nel tempo, separare le parti veloci da quelle lente può essere utile a gestire ciascuna nel modo più opportuno, così come può essere utile a capire come è composto il fenomeno.
Tra l'altro non è nemmeno strettamente indispensabile che il fenomeno sia periodico. Un fenomeno limitato nel tempo, per esempio un brano musicale, puoi pensare di metterlo in loop e analizzarlo come se fosse periodico. E' un po' una forzatura, ma può comunque essere molto utile a capire come è composto il fenomeno. Se un certo fenomeno non è periodico ma ha caratteristiche abbastanza stabili, puoi estrarne un pezzo, metterlo in loop come il brano, analizzarlo e usare il risultato come approssimazione del fenomeno generale. Un'altra utile forzatura. Insomma, un notevole strumento di analisi, che infatti ormai viene usato anche per fare il caffè.
Ancora però non si capisce perché è così importante il valore della fase iniziale per le varie sinusoidi che compongono il segnale di interesse. Per ora sembra un trucchetto matematico per far tornare i conti. Qui entra in gioco quella spiegazione che avevo dato per lo sweep logaritmico. Se prendo un qualunque sistema ad un ingresso e una uscita e con determinate caratteristiche di linearità e "stabilità" della funzione di trasferimento nel tempo posso caratterizzarlo completamente misurandone la risposta all'impulso. La risposta all'impulso mi determina esattamente come sono legati tra di loro ingresso e uscita, senza neanche bisogno di sapere in dettaglio come è fatto dentro il sistema. La risposta all'impulso però è anche un segnale, che posso dare in pasto alla trasformata di Fourier per capire come è "composta" la funzione di trasferimento del sistema. Qui la fase comincia ad avere un ruolo importante.
Dato che la rappresentazione nel dominio della frequenza è collegata in modo biunivoco con la risposta all'impulso, variando la fase puoi cambiare il comportamento temporale del sistema senza cambiarne la risposta in ampiezza. In sostanza si può dire che, a parità di risposta in ampiezza, la fase rappresenta nel dominio della frequenza il comportamento temporale del sistema.
Infatti, dalla fase, anzi, per essere più precisi, da come varia la fase in funzione della frequenza, si può determinare come il sistema ritardi l'inviluppo di "piccoli gruppi" di frequenze. Si può anche definire un'altro tipo di ritardo, chiamato ritardo di fase, e calcolando il limite del ritardo di fase con frequenza che va all'infinito si può estrarre il cosidetto "signal front delay", ossia il ritardo "minimo" tra ingresso e uscita, sotto il quale il sistema non può andare. Tra l'altro, questo è quello che lo stellatico intende quando parla di ritardo, solo che non lo sa, per cui quando si trova un sub a tromba che ha 100 ms di ritardo di gruppo all'estremo inferiore si inventa che è fisicamente impossibile perché la tromba è lunga solo pochi metri e quindi è un artefatto del sistema di misura, che era REW nel caso specifico, rimediando la solita figura da cioccolataio incompetente.
Un generico sistema inoltre può essere scomposto in due componenti, una a fase minima e una a fase in eccesso. Una scomposizione che di primo acchitto può sembrare un po' arbitraria, ma che è intimamente legata al comportamento fisico del sistema. La componente a fase minima in sostanza contiene le informazioni relative alla risposta in ampiezza, più quel minimo di risposta in fase che serve a mantenere il sistema causale. Ossia un sistema in cui il segnale esce dopo che è entrato, come avviene in tutti i sistemi fisici reali, mentre con la matematica si possono ipotizzare anche inesistenti sistemi che predicono il futuro. La componente a fase in eccesso ha risposta in ampiezza piatta, tecnicamente si dice che è un sistema all-pass, e contiene il resto della risposta in fase e quindi del comportamento temporale. I due sistemi messi in serie ti restituiscono il sistema originale, e analizzati separatamente ti danno ulteriori informazioni sulle caratteristiche del sistema.
Si può andare anche oltre e per esempio spezzettare un segnale in parti di breve durata da sottoporre separatamente a trasformata di Fourier, ottenendo informazioni ancora più dettagliate sull'andamento del segnale nel tempo, quello che probabilmente avrai già visto con il nome di spettrogramma. Questo è quello che fa, in prima rozza approssimazione, anche il nostro orecchio, ed essendo un'analisi nel tempo è per forza di cose una analisi sensibile alla fase, dato che la fase è andamento nel tempo. Questo è quello che lo stellatico non vuole capire, o fa finta di non capire, dato che vorrebbe dire ammettere l'ennesima figura da cioccolataio, e che rende un'affermazione apodittica come "la fase non si sente" una boiata stellare.
Qui mi fermo, sono già andato troppo oltre. La trasformata di Fourier, nelle sue varie versioni, e il concetto di fase che si porta dietro, ha millanta applicazioni teoriche e pratiche, che vanno dagli inutili effetti speciali di certi riproduttori di brani musicali ai più avanzati settori della fisica e della matematica. Ce n'è da riempire biblioteche intere, possibilmente cercando di evitare di turbare la tranquillità parigina.