Analisi Spettrale (cc)

[MarioBon]

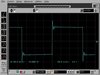
...l'inversione di due armoniche non cambia il risultato dell'analisi spettrale....
Lo dirò con parole mie senza "copiare dai libri" (qualcuno ci spiegherà da dove si dovrebbe copiare...).
Lo spettro di un segnale si ottiene sviluppando il segnale in serie di Fourier. Si usa la serie e non la trasformata perchè l'analizzatore di spettro, come strumento, tratta il segmento di segnale acquisito come se fosse un periodo di un segnale periodico. Lo spettro che ne ricava lo strumento è complesso: ha un parte reale e una parte immaginaria. Volendo, però, si può rappresentare uno spettro come modulo e fase o come prodotto dell'inviluppo per la fase istantanea (segnale analitico). Dato che tutti i suoni iniziano nel silenzio e finiscono nel silenzio e sono a media nulla sono sempre rappresentabili da un segnale analitico. A parte come si vuole rappresentare lo spettro non si deve confondere lo spettro con il suo modulo. La trasformarta (o la serie di Fourier) ha un senso perchè è unica (e questo è un teorema che si trova nei libri o anche qui: https://it.wikipedia.org/wiki/Trasformata_di_Fourier)

Se la rappresentazione di una funzione in serie di Fourier è unica significa che, eseguendo qualsiasi operazione che alteri lo spettro, si ottengono funzioni antitrasfomate (nel dominio del tempo) diverse. "Diverse" significa "non uguali". Quindi l'inversione o anche l'alterazione della fase di una singola armonica produce spettri diversi e quindi segnali diversi e quindi analisi spettrali diverse (udibili o non udibili qui non interessa).
Bisogna capire che "spettro" e "modulo dello spettro" non sono la stessa cosa.
Questa non è Elettroacustica e nemmeno Teoria dei Segnali, dei Sistemi o delle Reti: da quando sono stati formalizzati gli spazi vettoriali questa è Teoria degli Insiemi (quella che insegnao a partire dalle elementari): due insiemi che contengono gli stessi elementi sono lo stesso insieme (primo assioma di Zermelo).
Per contro due insiemi che contengono elementi diversi non sono lo stesso insieme.

Lo spettro di un segnale è l'insieme delle sue componenti complesse.
Due numeri complessi sono uguali se sono rispettivemente uguali le loro parti reali ed immaginarie.
Quindi è sufficiente dare una ripassata alla Teoria degli Insiemi ed in particolare alle strutture note come gruppi (una operazione) ed anelli (due operazioni) per arrivare alle strutture algebriche (tre operazioni). Gli spazi vettoriali sono strutture algebriche quindi questo sforzo è necessario.

P.S. nel documento che ho linkato viene utilizzata la parola "omomorfismo": le trasformazioni tra ingresso e uscita operate dai sistemi lineari sono omomorfismi. Per il resto i pasaggi algebrici non sono complicati.

[Ligo]

Certo, gruppi, anelli e ... campi!
Mannaggia, mi vien quasi voglia di riprendere qualche testo e rimettermi a sudiare .... quasi.

[TomCapraro]

Se la rappresentazione di una funzione in serie di Fourier è unica significa che, eseguendo qualsiasi operazione che alteri lo spettro, si ottengono funzioni antitrasformate (nel dominio del tempo) diverse. "Diverse" significa "non uguali". Quindi l'inversione o anche l'alterazione della fase di una singola armonica produce spettri diversi e quindi segnali diversi e quindi analisi spettrali diverse (udibili o non udibili qui non interessa).

Complimenti per il modo con cui riesci a "risalire" ai fenomeni.
Un vero piacere interloquire con veri conoscitori della materia.

Se avevi letto a calabrese gli avevo lasciato una "porta aperta" ovvero uno spiraglio dicendogli che il "trucco" c'era per poter vedere la diversità di spettro relativamente circoscritta al modello d'inviluppo che scaturisce dall'inversione di un armonica.

Come ben sai opero sempre con il "doppio confronto" (test ascolto ABX + misurazione)
Troverai le misure nella tua posta elettronica con tanto di descrizione...quasi quasi mi scoccia rivelare metodiche personali a gente che t'insulta.

[MarioBon]

In questo post Calabrese ammette un errore.
Poi però sottolinea una frase che non è corretta. L'inizio e la fine del segmento temporale da analizzare (finestra di acquisizione) non devono necessariamente coincidere con i passaggi del segnale per lo zero. Se fosse vero per analizzare una sinusoide basterebbe acquisirne mezzo periodo. E' necessario che il segmento scelto rappresenti un'intero periodo. L'analizzatore opera come se il segnale acquisito fosse un periodo di un ipotetico segnale contrariamente produrrebbe spettri continui (cosa che non sa e non può fare). Quindi, dato il segnale s(t), di periodo nT (dove T è il passo di campionamento e n il numero di campioni acquisiti) la finestra di acquisizione deve essere un multiplo intero di nT e deve deve risultare s(k) = s(k+nt) . Non ci sono particolari ipostesi sul valore di s(k) (istante di inizio della finestra di acquisizione). Va da sè che, per la FFT, n deve essere una potenza di due (cosa che si ttiene regolando T).
Le relazioni (differenze) di fase tra le componenti spettrali non dipendono dalla scelta della finestra di acquisizione (fatto salvo una eventuale componente proporzionale alla frequenza che può essere sottratta). Operando come detto, il segnale non coniene cuspidi ed è infinitamente derivabile (come lo è una serie di Fourier composta da un numero finito di righe).

Ancora una precisazione: l'analisi spettrale non si fa solo su segnali sonori. Il segnale che esce da un amplificatore, per esempio, non è un segnale sonoro (magari lo diventerà...) e comunque le definizioni, le regole e le proprietà dell'analisi spettrale sono sempre le stesse e non sono quelle dell'orecchio ma quelle che impone l'analizzatore di spettro (inteso come strumento).
Vi risparmio, anche se interessante, tutta la questione della relazione che lega l'osservabile all'osservato.
L'analizzatore di spettro, oggi molto diffuso e a basso costo, resta uno strumeno delicato e non facile da utilizzare. In particolare sono poco note le condizioni necessarie per ottenre una misura e non solo una stima dell spretto. Qualsiasi cosa si colleghi all'ingresso dell'analizzatre, il suo display mostra qualche cosa, ma da lì a dire che quello che si vede è lo spettro del segnale acquisito ce ne passa.
Misurare un spettro non è come misurare una tensione continua (anche ammesso non si faccia confusione tra Volt e Ampere).